[Python 로직과 순서도] 04.리스트 (정답)
연습문제
예제37
1부터 10까지의 수를 리스트에 저장하고 출력하기
i가 1부터 시작해 1씩 증가하며 10까지 반복하며 i 값을 리스트 a[ i-1 ]에 저장한다.
결국 a[0]에는 1, a[1]에는 2, a[2]에는 3, ..., a[9]에는 10이 저장된다.
분석 (설명)
- a(i-1)에 i 값을 저장한다.
- 배열 a를 출력한다.
설계 (순서도)

구현
a = []
for i in range(1, 11):
a.append(i)
print(a)
# 실행결과
# [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
예제38
10, 20, 30, ..., 100 저장하고, 거꾸로 출력하기
i가 1부터 1씩 증가하며 10이 될 때까지 반복하며 i*10을 a[i-1]에 저장한다. 그리고 i가 9부터 1씩 감소하며 0이 될 때까지 반복하며 a[i] 값을 출력한다.
분석 (설명)
- a(i-1)에 i*10을 저장한다. 결국 a(0)에는 10이, a(1)에는 20이, ..., a(9)에는 100이 저장된다.
- i 값이 9부터 1씩 감소하며 0이 될 때까지 반복한다.
- a(i) 요소를 출력한다
설계 (순서도)

구현
a = []
for i in range(10, 101, 10):
a.append(i)
for i in range(9, -1, -1):
print(a[i], end=" ")
# 실행결과
# 100 90 80 70 60 50 40 30 20 10
예제39
리스트 요소 거꾸로 뒤집기
i가 0부터 1씩 증가하며 4가 될 때까지 반복하며 a(i)와 a(9-i)를 교환한다. 결국 a[0]과 a[9]가, a[1]과 a[8]이, a[2]와 a[7]이, a[3]과 a[6]이, a[4]와 a[5]가 교환된다.
a 값과 b 값을 교환하는 절차는 다음과 같다.
temp = a
a = b
b = temp
분석 (설명)
- 배열 a를 초기화한다.
- a(i)와 a(9-i)를 교환한다.
설계 (순서도)

구현
a = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
for i in range(0, 5):
temp = a[i]
a[i] = a[9-i]
a[9-i] = temp
print(a)
# 실행결과
# [10, 9, 8, 7, 6, 5, 4, 3, 2, 1]
예제40
리스트 a 요소 리스트 b에 거꾸로 저장하기
리스트 a 요소를 거꾸로 해서 리스트 b에 저장한다.

i가 0부터 1씩 증가하며 9가 될 때까지 반복하며 a[9-i]값을 b[i]에 저장한다. 결국 b[0]에는 a[9] 값이, b[1]에는 a[8] 값이, ..., b[9]에는 a[0] 값이 저장된다.
분석 (설명)
- 배열 a를 초기화한다.
- b(i)에 a(9-i) 값을 저장한다
설계 (순서도)

구현
a = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
b = []
for i in range(0, 10):
b.append(a[9-i])
print(b)
# 실행결과
# [10, 9, 8, 7, 6, 5, 4, 3, 2, 1]
예제41
리스트 요소 왼쪽←으로 한 칸씩 원형으로 이동하기
리스트 요소를 왼쪽으로 한 칸씩 원형으로 이동하는 동작 전후 구조는 다음과 같다.

temp에 a[0] 값을 저장하고, i가 0부터 1씩 증가하며 8이 될 때까지 반복하며 a[i+1] 값을 a[i]에 저장한다.
그리고 temp 값을 a[9]에 저장한다.
분석 (설명)
- emp에 a(0) 값을 저장한다.
- a(i)에 a(i+1) 값을 저장한다.
- a(9)에 temp 값을 저장한다.
설계 (순서도)

구현
a = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
temp = a[0]
for i in range(0, 9):
a[i] = a[i+1]
a[9] = temp
print(a)
# 실행결과
# [2, 3, 4, 5, 6, 7, 8, 9, 10, 1]
예제42
리스트 요소 중 최댓값 구하기
a[0] 값을 max에 저장하고, i가 1부터 1씩 증가하며 9가 될 때까지 반복하며 a[i] 값이 max 값보다 크면 a[i] 값을 max에 저장한다.
Hint) 램덤한 값을 배열에 담는 방법
# random.randint를 사용하기 위해 random 모듈을 포함시킨다.
# random.randint(1,100)은 1부터 100까지의 정수 중 하나를 무작위로 선택한다.
import random
a = []
for i in range(10):
a.append(random.randint(1, 100))
print(a)
분석 (설명)
- max에 a(0) 값을 저장한다.
- max가 a(i) 보다 작은지 판별한다.
- max에 a(i) 값을 저장한다.
설계 (순서도)

구현
import random
a = []
for i in range(10):
a.append(random.randint(1, 100))
print(a)
m = a[0]
for i in range(1, 10):
if m<a[i]:
m = a[i]
print("최댓값:", m)
# 실행결과
# [91, 90, 78, 35, 65, 9, 97, 54, 62, 90]
# 최댓값: 97
예제43
에라토스테네스의 체 (선택 문제)
에라토스테네스의 체를 이용해서 1부터 100까지의 소수를 위 방법으로 구현하라.
그리스의 수학자이자 지리학자인 에라토스테네스가 고안한 소수를 찾는 방법이다.
이 방 법으로 소수를 찾으려면 2부터 시작해 자연수를 차례로 쓴 다음 2 이외의 2의 배수, 3 이외 의 3의 배수, 5 이외의 5의 배수의 순서로 수를 지워나가 끝에 남는 수가 소수이다.
그러면 체로 친 것처럼 끝에 남는 수가 있다.
이 수가 바로 그 자신과 1 이외의 다른 수로 는 나누어떨어지지 않는 소수이고, 이렇게 소수를 찾는 방법을 에라토스테네스의 체라고 한다.
에라토스테네스의 체를 이용해서 2부터 20까지의 소수를 찾는 예를 살펴보자
1. 시작수를 2로 한다.

2. 2를 제외한 2의 배수에 해당하는 수를 지운다.

3. 시작수를 3으로 한다.

4. 3을 제외한 3의 배수에 해당하는 수인 9와 15를 지운다.

5. 지워지지 않은 다음 수인 5가 시작수가 된다.

6. 5를 제외한 5의 배수에 해당하는 수를 지우고자 하는데 해당하는 수가 없다.

7. 시작수는 7, 11, 13, 17, 19로 변경되는데 이들 수의 배수에 해당하는 수는 없으므로 종료한다

8. 따라서 소수는 2, 3, 5, 7, 11, 13, 17, 19가 된다.
분석 (설명)
- 배열 a의 모든 요소에 0을 저장한다.
- i 값이 2부터 1씩 증가하며 100이 될 때까지 반복한다.
- a(i)가 0인지 판별한다.
- j 값이 i*2부터 i씩 증가하며 100이 될 때까지 반복한다. 결국 j는 i를 제외한 i 배수에 대 해 반복한다.
- a(j)에 1을 저장한다. a(j)에 1이 저장되면 j는 소수가 아님을 의미한다.
- i 값이 2부터 1씩 증가하며 100이 될 때까지 반복한다.
- a(i)가 0인지 판별한다. 0이면 i는 소수이다.
설계 (순서도)

구현
a = []
for i in range(1, 102):
a.append(0)
for i in range(2, 101):
if a[i]==0:
for j in range(i*2, 101, i):
a[j] = 1
for i in range(2, 101):
if a[i]==0:
print(i, end=" ")
# 실행결과
# 2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97
예제44
10진수를 2진수로 변환하여 리스트에 저장하기 (필수)
10진수를 입력받아, 2진수로 출력하는 프로그램을 개발하세요.
10진수를 2진수로 변환하는 과정을 이해하려면 진법의 개념을 먼저 이해해야 한다.
진법이란 사용할 수 있는 숫자의 개수와 위치 값을 정의해주는 수 체계이다.
한 자리에 사용할 수 있는 숫자의 개수는 해당 진법과 같으며, 사용할 수 있는 숫자는 0에서 시작해서 해당 진법의 수보다 1적은 수까지 가능하다.
그러므로 10진법에서 사용할 수 있는 숫자는 0, 1, 2, …, 8, 9로 10개가 되고, 2진법에서는 0과 1로 2개를 사용할 수 있다.
16진법과 같이 10진법보다 큰 진법의 경우에는 0부터 9까지의 수 외에도 다른 수가 더 필요한데 이런 경우에 A, B, C, D, E, F를 사용한다. 16진법의 A는 10진수 10을, B는 10진수 11을, …, F는 10진수 15를 의미한다.
컴퓨터에서 많이 사용되는 10진수, 2진수, 8진수 16진수의 관계를 표로 나타내면 다음과같다.

| 10진수 | 2진수 | 8진수 | 16진수 |
| 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
| 2 | 10 | 2 | 2 |
| 3 | 11 | 3 | 3 |
| 4 | 100 | 4 | 4 |
| 5 | 101 | 5 | 5 |
| 6 | 110 | 6 | 6 |
| 7 | 111 | 7 | 7 |
| 8 | 1000 | 10 | 8 |
| 9 | 1001 | 11 | 9 |
| 10 | 1010 | 12 | A |
| 11 | 1011 | 13 | B |
| 12 | 1100 | 14 | C |
| 13 | 1101 | 15 | D |
| 14 | 1110 | 16 | E |
| 15 | 1111 | 17 | F |
| 16 | 10000 | 20 | 10 |

다음으로 진수 변환을 알아보자. 먼저 10진수를 2진수 또는 8진수로 변환하는 내용에 대해 살펴보자.
10진수를 다른 진수로 변환하려면 10진수를 변환하고자 하는 진수로 몫이 0이 될 때까지계속해서 나누고 나머지를 역순으로 나열한 값이 변환한 값이 된다.
예를 들어 37을 2진수로 변환하려면 다음과 같이 37을 2로 계속해서 나눈다. 그리고 나머지를 역순으로 배열하면 100101이 되는데 이 값이 10진수 37을 2진수로 변환한 값이 된다.

또 다른 예로 10진수를 8진수로 변환하는 과정은 다음과 같다. 10진수 87을 8진수로 변환
하면 127이다.
10진수를 2진수로 변환하려면 10진수를 2로 나누어 나머지를 구하고, 몫을 2로 다시 나누어 나머지를 구하는 동작을 반복한다. 몫이 0이 되면 반복을 중단하고, 구한 나머지를 역순으로 나열한 값이 결과 값이 된다.
분석 (설명)
- n이 0이 아닌지 판별한다.
- 10진수 n을 2로 나눈 나머지를 b(a)에 저장한다.
- 배열 b에 저장된 내용을 거꾸로 출력하기 위해 i 값이 a-1부터 1씩 감소하며 0이 될 때 까지 반복한다.
설계 (순서도)

구현
b = []
n = int(input("10진수: "))
while n!=0:
b.append(n%2)
n = n//2
for i in range(len(b)-1, -1, -1):
print(b[i], end=" ")
# 실행결과
# 10진수 : 42
# 1 0 1 0 1 0
예제 45
배열에 저장된 2진수를 10진수로 변환하기
2진수를 한자리 10진수를 출력하는 프로그램을 만드세요.
2진수를 10진수로 변환하는 내용에 대해 살펴보자.
수 체계에 있어서 중요한 개념 중 하나는 자리 값인데, 모든 수의 각 숫자는 자리 값을가지고 있다.
각 숫자의 자리 값은 그 위치가 의미하는 제곱수를 해당 진법에 적용하면되는데, 각 위치가 의미하는 제곱수는 가장 오른쪽이 0이고 왼쪽으로 가면서 1을 더한 값이 된다.
예를 들면, 2진수 11001은 다음과 같은 절차를 거쳐 10진수 25가 된다.
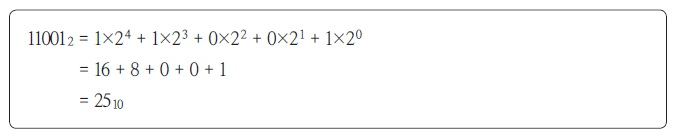
이와 같이 2진수를 10진수로 변환할 때는 2진수 각 자리를 10진수로 변환하여 모두 더하면 된다.
단, 2진수는 5자리라 가정한다.
분석 (설명)
- 2진수 b(i)를 10진수로 변환해서 n에 누적한다. 2**(4-i)는 2 4-i 를 의미한다.
설계 (순서도)

구현
b = [1,1,0,0,1]
n = 0
for i in range(0, 5):
n = n + b[i]*(2**(4-i))
print(n)
# 실행결과
# 25 # (2진수 리스트가 b = [1,1,0,0,1] 일 때)
예제46
선형 탐색 알고리즘
임의의 숫자를 10개를 요소로 가지는 리스트를 만들고, 키 값을 입력했을 때 인덱스를 찾아 출력하는 선형 탐색 알고리즘을 구현하라.
탐색이란?
컴퓨터에 저장된 데이터 집합에서 어떤 조건이나 성질을 만족하는 데이터를 찾는것이다.
탐색하고자 하는 데이터는 무작위로 섞여있는 데이터와 특정한 규칙에 따라 정렬된 데이터로 구분할 수 있다.
데이터의 유형에 따라 적합한 탐색 방법이 있는데, 우선 무작위로 섞여있는 데이터를 탐색하는 방법인 선형 탐색에 대해 살펴보자.
선형 탐색은 순차 탐색이라고도 하는데, 주어진 데이터 집합에서 원하는 데이터를 처음부터 순차적으로 비교하면서 찾는 방법이다.
다음 데이터 집합에서 선형 탐색을 이용해서 데이터 7을 탐색하는 과정을 알아보자.

① 첫 번째 데이터인 15와 7을 비교한다. 값이 다르므로 다음으로 이동한다.

② 두 번째 데이터인 19와 7을 비교하는데, 다르므로 다음으로 이동한다.

③ 세 번째 데이터인 5와 7을 비교하는데, 다르므로 다음으로 이동한다.

④ 네 번째 데이터인 7과 찾고자 하는 3이 같으므로 원하는 데이터를 찾고 탐색을 종료한다.

만약 마지막까지 찾는 데이터가 없으면 탐색 실패를 알려주고 끝내야 한다.
분석 (설명)
- cnt가 10보다 작은지 판별한다.
- key와 a(cnt)가 같은지 판별한다.
- cnt가 10이 될 때까지 찾지 못하면 “탐색실패”를 출력한다
설계 (순서도)

구현
a = [26, 27, 39, 63, 57, 75, 11, 76, 80, 18]
key = int(input("키: "))
cnt = 0
while cnt<10:
if key == a[cnt]:
print(cnt, "에서 탐색 성공")
break
cnt = cnt+1
if cnt == 10:
print("탐색 실패")
# 실행결과
# 키: 11
# 6 에서 탐색 성공 (a = [26, 27, 39, 63, 57, 75, 11, 76, 80, 18] 리스트 일 때)
예제47
이진 탐색 알고리즘
임의의 숫자를 10개를 요소 또는 예시(a = [11, 18, 26, 27, 39, 57, 63, 75, 76, 80])와 같은 리스트를 만들고, 키 값을 입력했을 때 인덱스를 찾아 출력하는이진 탐색 알고리즘을 구현하세요.
이진 탐색은 정렬된 데이터 집합을 이분화하면서 탐색하는 방법이다.
① 다음 데이터 집합에서 이진 탐색을 이용해서 데이터 9를 탐색하는 과정을 알아보자.

② 중간에 위치한 데이터인 7과 9를 비교한다.

③ 중간에 위치한 데이터인 7보다 찾고자 하는 데이터인 9가 크므로 7보다 오른쪽에 위치한 데이터들에 대해 이진 탐색을 수행한다. 새로운 탐색 영역의 중간에 위치한 11과 9를 비교한다.

④ 11보다 9가 작으므로 11보다 왼쪽에 위치한 데이터들에 대해 다시 한번 이진 탐색을 수행한다. 새로운 탐색 영역의 중간에 위치한 9와 9를 비교한다. 찾고자 하는 데이터이므로 탐색을 종료한다.

⑤ 마찬가지로 마지막까지 찾는 데이터가 없으면 탐색 실패로 끝낸다.
분석 (설명)
- 탐색 범위의 시작 첨자인 low에 0을, 마지막 첨자인 high에 9를 저장한다.
- low가 high이하인지 판별한다.
- low와 high의 평균을 구해 mid에 저장한다. low+high를 2로 나눈 몫이 mid에 저장된다.
- key와 a(mid)가 같은지 판별한다.
- key가 a(mid) 보다 작은지 판별한다. 작으면 low에 mid+1을 저장하고, 크면 high에 mid-1을 저장한다.
설계 (순서도)

구현
a = [11, 18, 26, 27, 39, 57, 63, 75, 76, 80]
key = int(input("키 : "))
low = 0
high = 9
while low<=high:
mid = (low+high)//2
if key == a[mid]:
print(mid, "에서 탐색 성공")
break
elif key < a[mid]:
high = mid-1
else:
low = mid+1
if low > high:
print("탐색 실패")
# 실행결과
# 키 : 39
# 4 에서 탐색 성공
예제48
선택 정렬 알고리즘
임의의 리스트에 요소를 원하는 만큼 무작위로 넣고, 선택 정렬 알고리즘을 구현하여 정렬하세요
순서에 상관없이 배열된 데이터를 일정 규칙에 따라 배열하는 것을 정렬이라 하는데, 엑셀은 물론이고 글을 비롯한 많은 소프트웨어에 정렬 기능이 있다.
정렬을 하는 방법은 여러 가지가 있는데, 그 중 선택 정렬에 대해 살펴보자.
선택 정렬은 정렬되지 않은 데이터들에 대해 가장 작은 데이터를 찾아 가장 앞의 데이터와교환해가는 방식이다.
그러면 선택 정렬의 동작 과정을 다음 데이터를 이용해서 살펴보자.

① 가장 앞에 위치(기준 위치)한 15와 가장 작은 데이터인 1을 교환한다. 가장 작은 데이터가 가장 앞에 위치하게 된다.

② 첫 번째 데이터를 제외한 나머지 데이터에서 가장 작은 데이터인 3과 두 번째에 위치(기준 위치)한 데이터인 11을 교환한다.

③ 첫 번째, 두 번째 데이터를 제외한 나머지 데이터에서 가장 작은 데이터인 8과 세 번째에 위치(기준 위치)한 데이터인 15를 교환한다.

④ 첫 번째, 두 번째, 세 번째 데이터를 제외한 나머지 데이터에서 가장 작은 데이터인 11과 네 번째 위치(기준 위치)한 데이터인 11을 교환한다. 같은 데이터이므로 위치의 변화는 없다. 데이터들에 대한 정렬이 완료된다.

분석 (설명)
- i 값이 0부터 1씩 증가하며 4가 될 때까지 반복한다.
- j가 i+1부터 1씩 증가하며 5가 될 때까지 반복한다.
- a(i)와 a(min)을 교환한다.
설계 (순서도)

구현
a = [20, 50, 30, 10, 60, 40]
for i in range(0, 5):
m = i
for j in range(i+1, 6):
if a[j]<a[m]:
m = j
temp = a[i]
a[i] = a[m]
a[m] = temp
print(a)
# 실행결과
# [10, 20, 30, 40, 50, 60] (a =[20, 50, 30, 10, 60, 40] 리스트 일 때)
예제49
버블 정렬 알고리즘
임의의 리스트에 요소를 원하는 만큼 무작위로 넣고, 버블 정렬 알고리즘을 구현하여 정렬하라
버블 정렬은 서로 이웃한 데이터들을 비교하며 가장 큰 데이터를 가장 뒤로 보내며 정렬하는 방식이다.
버블 정렬의 동작 과정을 다음과 같은 데이터를 이용해서 살펴보자.

① 첫 번째 데이터인 15와 두 번째 데이터인 11을 비교해 큰 데이터를 뒤로 위치시킨다. 15가 크므로 둘의 위치를 바꾼다.

② 두 번째 데이터인 15와 세 번째 데이터인 1을 비교하는데, 앞에 위치한 15가 크므로 둘의 위치를 바꾼다.

③ 마찬가지 방식을 적용해 세 번째 데이터인 15와 네 번째 데이터인 3의 위치를 바꾼다.

④ 네 번째 데이터인 15와 마지막 데이터인 8의 위치를 바꾼다. 가장 큰 데이터인 15가 가장 뒤에 위치하게 된다

⑤ 처음부터 다시 시작한다. 첫 번째 데이터인 11과 두 번째 데이터인 1의 크기를 비교하는데 앞에 위치한 11이 크므로 둘의 위치를 바꾼다.

⑥ 두 번째 데이터인 11과 세 번째 데이터인 3의 위치를 바꾼다.

⑦ 세 번째 데이터인 11과 네 번째 데이터인 8의 위치를 바꾼다. 두 번째로 큰 데이터인 11이 뒤에서 두 번째에 위치하게 된다.

⑧ 처음부터 다시 시작한다. 첫 번째 데이터인 1과 두 번째 데이터인 3의 크기를 비교하는데앞에 위치한 1이 작으므로 그대로 둔다.

⑨ 두 번째 데이터인 3과 세 번째 데이터인 8의 크기를 비교하는데, 앞에 위치한 3이 작으므로 그대로 둔다. 세 번째로 큰 데이터인 8이 뒤에서 세 번째에 위치하게 된다.

⑩ 처음부터 다시 시작한다. 첫 번째 데이터인 1과 두 번째 데이터인 3의 크기를 비교하는데, 앞에 위치한 1이 작으므로 그대로 둔다. 데이터들에 대한 정렬이 완료된다

분석 (설명)
- i 값이 0부터 1씩 증가하며 4가 될 때까지 반복한다.
- j 값이 0부터 1씩 증가하며 4-i가 될 때까지 반복한다.
- a(j)가 a(j+1)보다 큰지 판별한다.
- a(j)와 a(j+1)을 교환한다.
설계 (순서도)

구현
a = [20, 50, 30, 10, 60, 40]
for i in range(0, 5):
for j in range(0, 5-i):
if a[j]>a[j+1]:
temp = a[j]
a[j] = a[j+1]
a[j+1] = temp
print(a)
# 실행결과
# [10, 20, 30, 40, 50, 60] (a =[20, 50, 30, 10, 60, 40] 리스트 일 때)
예제50
병합 정렬 알고리즘
임의의 리스트 2개에 요소를 원하는 만큼 무작위로 넣고, 병 정렬 알고리즘을 구현하여 정렬하세요.
병합 정렬은 정렬된 두 개의 데이터 집합을 하나의 정렬된 데이터 집합으로 만드는 방법으로, 동작 과정을 다음과 같은 정렬된 데이터 집합인 배열 a와 배열 b에 대해 살펴보자.

① a(0)인 1이 b(0)인 3보다 작으므로 a(0) 값인 1을 c(0)에 저장한다.

② a(1)인 3이 b(0)인 3보다 작지 않으므로 b(0) 값인 3을 c(1)에 저장한다.

③ a(1)인 3이 b(1)인 4보다 작으므로 a(1) 값인 3을 c(2)에 저장한다.

④ a(2)인 5가 b(1)인 4보다 작지 않으므로 b(1) 값인 4를 c(3)에 저장한다.

⑤ a(2)인 5가 b(2)인 8보다 작으므로 a(2) 값인 5를 c(4)에 저장한다.

⑥ a(3)인 7이 b(2)인 8보다 작으므로 a(3) 값인 7을 c(5)에 저장한다.

⑦ 배열 a의 모든 요소가 배열 c에 저장되었으므로 배열 b의 남은 요소인 8과 10을 순서대로 배열 c에 저장한다. 모든 데이터들에 대한 정렬이 완료된다.

분석 (설명)
- 배열 a와 b를 초기화한다.
- i가 4미만이고 j가 4미만인지 판별한다.
- a(i)가 b(j)보다 작은지 판별한다.
- a(i)를 c(k)에 저장하고 i 값과 k 값을 1 증가시킨다.
- b(j)를 c(k)에 저장하고 j 값과 k 값을 1 증가시킨다.
- i가 4와 같은지 판별한다.
설계 (순서도)

구현
a = [1, 3, 5, 7]
b = [3, 4, 8, 10]
c = []
i = 0
j = 0
while i<4 and j<4:
if a[i]<b[j]:
c.append(a[i])
i = i+1
else:
c.append(b[j])
j = j+1
if i==4:
while j<4:
c.append(b[j])
j = j+1
else:
while i<4:
c.append(a[i])
i = i+1
print(c)
# 실행결과
# [1, 3, 3, 4, 5, 7, 8, 10]
과제
과제 28
20부터 1까지 수를 차례로 리스트에 저장하고 출력하는 순서도와 파이썬 프로그램을 작성하여라.
설계 (순서도)

구현
a = []
for i in range(10, 0, -1):
a.append(i)
print(a)
# 실행결과
# [10, 9, 8, 7, 6, 5, 4, 3, 2, 1]
과제 29
리스트 요소를 오른쪽으로 한 칸씩 원형으로 이동하는 순서도와 파이썬 프로그램을 작성하여라.
리스트 예) a = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
설계 (순서도)

구현
a = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
temp = a[9]
for i in range(9, 0, -1):
a[i] = a[i-1]
a[0] = temp
print(a)
# 실행결과
# [10, 1, 2, 3, 4, 5, 6, 7, 8, 9]
과제 30
임의의 10개의 수를 저장하고 있는 리스트에서 최솟값을 구하는 순서도와 파이썬 프로그램을 작성하여라.
# 임의의 값 리스트에 담기
import random
a = []
for i in range(10):
a.append(random.randint(1, 100))
print(a)
설계 (순서도)

구현
import random
a = []
for i in range(10):
a.append(random.randint(1, 100))
print(a)
m = a[0]
for i in range(1, 10):
if m>a[i]:
m = a[i]
print("최솟값:", m)
# 실행결과
# [54, 25, 63, 32, 7, 27, 82, 75, 11, 4]
# 최솟값: 4
과제 31
입력 받은 10진수를 8진수로 변환하여 출력하는 순서도와 파이썬 프로그램을 작성하여라.
설계 (순서도)

구현
o = []
n = int(input("10진수: "))
while n!=0:
o.append(n%8)
n = n//8
for i in range(len(o)-1, -1, -1):
print(o[i], end=" ")
# 실행결과
# 10진수: 39
# 4 7
과제 32
리스트에 저장된 8진수를 10진수로 변환하는 순서도와 파이썬 프로그램을 작성하여라.
예) 8진수 56743 을 리스트 [5,6,7,4,3] 와 같이 입력하여 / 10진수로 변환
설계 (순서도)

구현
o = [5,6,7,4,3]
n = 0
for i in range(0, 5):
n = n + o[i]*(8**(4-i))
print(n)
# 실행결과
# 24035
과제 33
내림차순으로 정렬된 데이터 집합에 대한 이진 탐색을 하는 순서도와 파이썬 프로그램을 작성하여라.
리스트 예) a = [80, 76, 75, 63, 57, 39, 27, 26, 18, 11]
설계 (순서도)

구현
a = [80, 76, 75, 63, 57, 39, 27, 26, 18, 11]
key = int(input("키 : "))
low = 0
high = 9
while low<=high:
mid = (low+high)//2
if key == a[mid]:
print(mid, "번째 인덱스에서 탐색 성공")
break
elif key > a[mid]:
high = mid-1
else:
low = mid+1
if low > high:
print("탐색 실패")
# 키 : 26
# 7 번째 인덱스에서 탐색 성공
과제 34
삽입 정렬은 다음과 같이 이미 정렬된 부분에서 자신의 위치를 찾아 삽입하며 정렬하는 방식이다.
삽입 정렬을 이용해서 정렬하는 순서도와 파이썬 프로그램을 작성하여라
리스트 예) a = [3, 7, 2, 8, 5, 1, 10, 9, 4, 6]
설계 (순서도)

구현
a = [3, 7, 2, 8, 5, 1, 10, 9, 4, 6]
for i in range(1, 10):
key = a[i]
j = i-1
while j>=0:
if key<a[j]:
a[j+1] = a[j]
else:
break
j = j-1
a[j+1] = key
print(a)
# 실행결과
# [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]