[Python 로직과 순서도] 05.함수 (정답)

연습문제

예제51

함수 이용해서 두 수 중 큰 수 찾기

두 수를 입력받고, 그 중 큰 수를 찾아 반환한다.

반환하는 로직은 func 함수를 정희하고 사용해서 두 수 중 큰 수를 찾는다.

분석 (설명)

a, b 중 큰 수를 반환하는 func 함수를 정의한다.
m 값을 반환한다.
func 함수를 호출한다. 이 때 a, b 값이 전달된다. 그리고 func 함수에서 반환한 값을 r 에 저장한다.

설계 (순서도)

구현

def func(a,b):
    if a>b:
        return a
    else:
        return b
a = int(input("정수: "))
b = int(input("정수: "))
r = func(a, b)
print(r)

# 실행결과
# 정수: 7
# 정수: 3
# 7

# 로직 참고
# a, b 중 큰 수를 반환하는 func 함수를 정의한다.
# a 값을 반환한다.
# b 값을 반환한다.
# func 함수를 호출하고, func 함수에서 반환된 값을 r에 저장한다.

예제52

함수 이용해서 세 수 중 큰 수 찾기

세 수 중 큰 수를 찾아 반환하는 func 함수를 이용해서 세 수 중 큰 수를 찾는다.

분석 (설명)

a, b, c 중 가장 큰 수를 반환하는 func 함수를 정의한다.
m 값을 반환한다.
func 함수를 호출한다. 이 때 a, b, c 값이 전달된다. 그리고 func 함수에서 반환한 값을 r에 저장한다.

설계 (순서도)

구현

def func(a,b,c):
    if a>b:
        if a>c:
            return a
        else:
            return c
    else:
        if b>c:
            return b
        else:
            return c
a = int(input("정수: "))
b = int(input("정수: "))
c = int(input("정수: "))
r = func(a, b, c)
print(r)

# 실행결과
정수: 4
정수: 7
정수: 5
7

# 로직 참고
# a, b, c 중 가장 큰 수를 반환하는 func 함수를 정의한다.
# func 함수를 호출하고, func 함수에서 반환된 값을 r에 저장한다.

예제53

함수 이용해서 1부터 10까지의 약수 구하기

임의의 수에 대한 약수 구하는 func 함수를 이용해서 1부터 10까지의 수에 대한 약수를 구한다.

분석 (설명)

a의 약수를 구하는 func 함수를 정의한다.
func 함수를 종료한다.

설계 (순서도)

구현

def func(a):
    for i in range(1, a+1):
        if a%i==0:
            print(i, end=" ")
for i in range(1, 11):
    print(i, ":", end=" ")
    func(i)
    print()

# 실행결과
# 1 : 1 
# 2 : 1 2 
# 3 : 1 3 
# 4 : 1 2 4 
# 5 : 1 5 
# 6 : 1 2 3 6 
# 7 : 1 7 
# 8 : 1 2 4 8 
# 9 : 1 3 9 
# 10 : 1 2 5 10 
# 7

# 로직 참고
# a의 약수를 구하는 func 함수를 정의한다.
# func 함수를 호출한다. 이 때 i 값을 전달한다.

예제54

재귀함수 이용해서 1부터 입력 받은 수까지의 합 구하기

재귀함수를 사용하는 방법을 알아보겠습니다.

1부터 3까지의 합은 다음과 같습니다.

3 + 2 + 1

이것을 다음과 같이 나타낼 수 있습다.

3 + 1부터 2까지의 합

여기서 ‘1부터 3까지의 합’을 함수 호출 형식으로 다음과 같이 나타낼 수 있다.

sum(3)

sum(3)은 다음과 같은 의미를 지닌다

3 + sum(2)

3을 a로 일반화 시키면 다음과 같은데 1부터 a까지의 합을 의미한다

sum(a) = a + sum(a - 1)

그런데 1부터 1까지의 합은 1이므로 a가 1인 경우에는 1이 된다

sum(1) = 1

이런 내용을 포함해서 다시 정리하면 다음과 같다.

sum(a) = 1 (n ≤ 1)

= a + sum(a - 1) (그 외)

이런 개념을 이용해서 1부터 임의의 수까지의 합을 구하는 sum 재귀함수를 만들어서 1부 터 입력 받은 수까지의 합을 구한다.

분석 (설명)

a의 약수를 구하는 func 함수를 정의한다.
func 함수를 종료한다.

설계 (순서도)

구현

def s(a):
    if a<=1:
        return 1
    return a+s(a-1)

n = int(input("정수: "))
result = s(n)
print(result)

# 실행결과
# 정수: 10
# 55

예제55

재귀함수 이용해서 피보나치수열 구하기

피보나치수열의 a번째 항은 다음과 같다.

fibo(a) = 1 (a≤2)

= fibo(a-1) + fibo(a-2) (그 외)

이런 개념을 이용해서 피보나치수열의 임의의 항을 구하는 fibo 재귀함수를 만들어서 입력 받은 위치에 대한 피보나치수를 구한다.

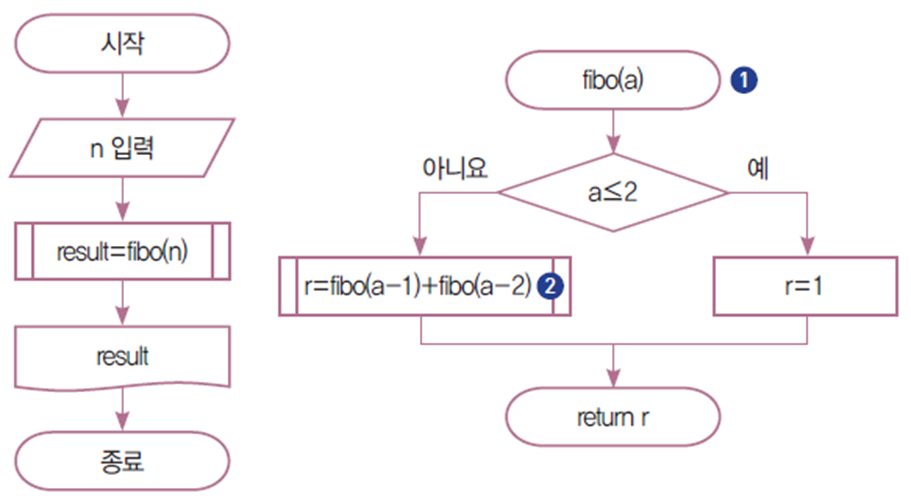
분석 (설명)

피보나치수열의 a번째 항을 구하는 fibo 함수를 정의한다.
2 fibo 함수를 재귀호출한다.

설계 (순서도)

구현

def fibo(a):
    if a <=2:
        return 1
    return fibo(a-1)+fibo(a-2)

n = int(input("정수: "))
result = fibo(n)
print(result)

# 실행결과
# 정수: 7
# 13

# 로직 참고
# 피보나치수열의 a번째 항을 구하는 fibo 함수를 정의한다.
# fibo 함수를 재귀호출한다. 
# fibo 함수를 호출하고, fibo 함수에서 반환된 값을 result에 저장한다.

과제

과제 35

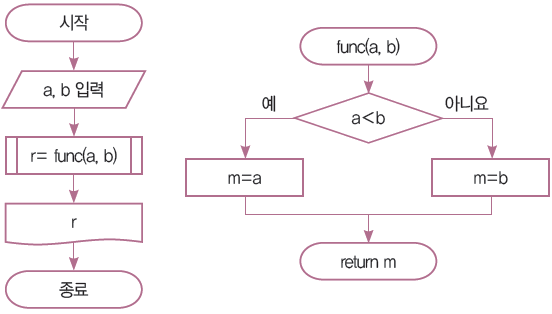
함수를 이용해서 두 수중 작은 수를 찾는 순서도와 파이썬 프로그램을 작성 하여라.

설계 (순서도)

구현

def func(a,b):
    if a<b:
        return a
    else:
        return b

a = int(input("정수: "))
b = int(input("정수: "))
r = func(a, b)
print(r)

# 실행결과
# 정수: 100
# 정수: 60
# 60

과제 36

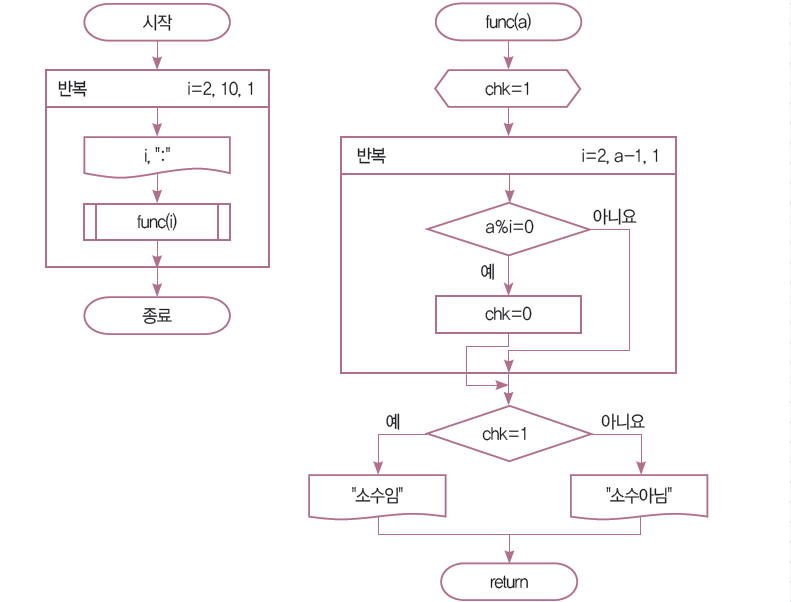
소수 판별하는 함수를 이용해서 2부터 10까지의 수에 대해 소수인지 아닌지를 출력하는 순서도와 파이썬 프로그램을 성하여라.

설계 (순서도)

구현

def func(a):
    chk = 1
    for i in range(2, a):
        if a%i == 0:
            chk = 0
            break
    if chk==1:
        print(a, ": 소수임")
    else:
        print(a, ": 소수아님")
        
for i in range(2, 11):
    func(i)

# 실행결과
# 2 : 소수임
# 3 : 소수임
# 4 : 소수아님
# 5 : 소수임
# 6 : 소수아님
# 7 : 소수임
# 8 : 소수아님
# 9 : 소수아님
# 10 : 소수아님

과제 37

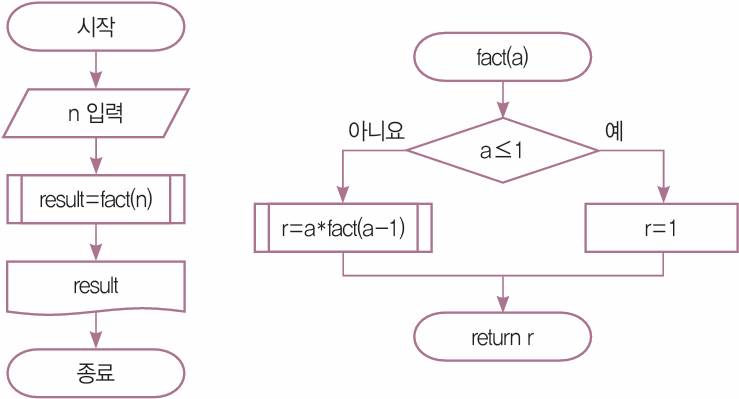
계승을 구하는 재귀함수를 이용해서 입력 받은 수에 대한 계승을 구하는 순서도와 파이썬 프로그램을 작성하여라.

설계 (순서도)

구현

def f(a):
    if a<=1:
        return 1
    return a*f(a-1)

n = int(input("정수: "))
result = f(n)
print(result)

# 실행결과
# 정수: 10
# 3628800

티스토리툴바